论文笔记：Few-Shot Learning

• 数据增强和正则化技术能减轻数据很少时的过拟合状况，但是不能算是解决了它。

  所谓的 Few-Shot Learning 也不能算解决啊，也没有什么方法敢说是解决了。

• 非参数化模型（如最近邻方法）能直接用已有的数据作为先验来对新的数据进行分类，也能快速地适应新的类别，这种优点值得借鉴

  考虑分类这个问题，非参数化模型的问题在于它需要将先验数据存储下来进行比对，当数据量很大时会有效率问题；另外就是现有的一些非参数化模型，往往只能使用一些通用的度量方法，往往会有泛化性问题。Few-Shot Learning 某种程度上来说确实算是借鉴了非参数化模型的思路，用 support set 作为先验知识，然后在度量计算上使用可训练的模块。

• 论文作者认为，如果实际处理的数据和训练用数据的分布相差较大时，论文中提出的模型可能会没啥效果

模型的大致结构是这样的

Given Support Set \(S={(x_{i}, y_{i})}_{i=1}^{k}\) ——由于本文讨论的 One-shot 的，所以 support 里的每个样本的类别也就是 \(y_{i}\) 都是不同的。

任给 \(\hat{x}\)，将它预测为 \(y_{i}\) 的概率为 \(P(y_{i}|\hat{x}, S)\)，最大概率的预测也就是 \(\mathop{\arg\max}\limits_{y}P(y|\hat{x}, S)\)

Few-Shot Learning 要学习的，就是这个 \(P\)。

如果用一个向量来表示预测输出的话（这也是通常做法），用 one hot 向量来表示每一个 \(y_{i}\) 的话，那么模型就可以写成

\[\hat{y} = \sum_{i=1}^{k}a(\hat{x}, x_{i})y_{i}\qquad (x_{i}, y_{i})\in S\]

这里的 \(a\) 可以是一个 attention 模块，其定义为

\[a(\hat{x}, x_{i})=\frac{e^{c(f(\hat{x}), g(x_{i}))}}{\sum_{j=1}^{k}e^{c(f(\hat{x}), g(x_{j}))}}\]

其中 \(f\) 和 \(g\) 都是一个 embedding 函数，在不同的任务上会不一样，比如在 NLP 任务上可以是一个 word embedding，在图像任务上则可以是一个 CNN 网络层；匹配函数 \(c(\cdot, \cdot)\) 则用来计算两个 embedding 的相关度，它可以是任意一个距离度量方法或相似度量方法，也可以是一个神经网络模块。

在模型上，这篇论文针对 embedding 函数 \(f\) 和 \(g\) 做了一些特殊设计，文中称为 Full Context Embedding，简称 FCE ；而匹配函数 \(c(\cdot, \cdot)\) 则统一使用 cosine 方法。下面则来看看这个 Full Context Embedding。

所谓 Context 指的是 support set \(S\)；进一步的，所谓的 Full Context Embedding，意思就是说，在计算 embedding 的时候，也要用到 \(S\)，而不是简单将数据输入到一个网络模块中然后得到一个表示向量。这个思想和观点，怎么说呢，熟悉 attention 机制的话应该不会觉得陌生。

\(f\) 的 FCE 版本定义如下：

\[f(\hat{x}, S) = attLSTM(f^{\prime}(\hat{x}), g(S), K)\]

其中 \(f^{\prime}\) 是一个单纯的编码器，可以是任意一种合适的神经网络，其输入只有 \(\hat{x}\)，\(g(S)\) 是所有 \(g(x_{i})\) 的简化表示。\(K\) 表示处理步骤数 —— 打个比方，就是hi把 \(f^{\prime}(\hat{x})\) 重复 \(K\) 次作为 LSTM 的 \(K\) 个 timestep 的输入，然后用这 \(K\) 个 timestep 的 hidden state 输出和 \(g(S)\) 做 attention 计算，具体来说，在第 \(k\) 步，有：

\[\hat{h_{k}},c_{k} = LSTM(f^{\prime}(\hat{x}), [h_{k-1},r_{k-1}], c_{k-1})\]

\[h_{k}=\hat{h_{k}} + f^{\prime}(\hat{x})\]

\[r_{k-1}=\sum_{i=1}^{|S|}a(h_{k-1}, g(x_{i}))g(x_{i})\]

\[a(h_{k-1}, g(x_{i}))=softmax(h_{k-1}^{T}g(x_{i}))\]

注意：上面的 \(k\) 与 support set 的大小 \(k\) 无关，仅仅是一个符号表示上的巧合。

除了对 \(f\) 做改进外，\(g\) 也有 FCE 版本，如下所示：

\[g(x_{i}) = \overrightarrow{h}_{i} + \overleftarrow{h}_{i} + g^{\prime}(x_{i})\]

\[\overrightarrow{h}_{i}, \overrightarrow{c}_{i} = LSTM(g^{\prime}(x_{i}), \overrightarrow{h}_{i-1}, \overrightarrow{c}_{i-1})\]

\[\overleftarrow{h}_{i}, \overleftarrow{c}_{i} = LSTM(g^{\prime}(x_{i}), \overleftarrow{h}_{i+1}, \overleftarrow{c}_{i+1})\]

其中 \(g^{\prime}\) 和 \(f^{\prime}\) 类似，剩下的部分也很好理解，相当于把 \(g^{\prime}(x_{0})\ldots g^{\prime}(x_{k})\) 当作序列作为一个 BiLSTM 的输入了。

使用了 Omniglot 数据集、ImageNet 数据集和 Penn Treebank 三个数据集分别去和其他模型做对比实验，大致上，在三个数据集上，都是先划分出类别完全不交叉的训练集和测试集然后进行训练和测试，对测试的细节没有说清楚，我所谓的没说清楚包括：

• 前面的模型部分都是以 one-shot 为背景来说的，但实验中却有 5-shot 的情况，模型在 5-shot 的时候是怎样的？直接将每个类别的 embedding 平均？
• Few-Shot Learning 的测试有别于普通的分类问题，一般来说是多次采样出 support set 和 query set 进行测试，然后对多次采样结果进行平均，那么，采样多少次，是否覆盖了测试集中的大部分数据？

在 Omniglot 数据集上实验时，对比用的模型有：

• PIXELS: 直接用图像的像素值做匹配
• BASELINE CLASSIFIER: 先在训练集上做训练，由于普通的分类器并不能识别测试集中未见过的类别，所以训练完后测试时，用模型最后一层的输出作为图像的特征向量，然后去进行匹配
• MANN: 一篇关于 Meta Learning 论文中²提出的模型
• CONVOLUTIONAL SIAMESE NET³
• MATCHING NETS: 这篇论文提出的模型

下面是在 Omniglot 数据集上的对比结果：

我的疑惑：

• BASELINE CLASSIFIER 的第三个模式用的 Matching Fn 是 Softmax，是什么意思？ softmax 函数不是用来做匹配或者相似计算的呀？
• MATCHING NETS 的 embedding 部分具体用的什么结构，单层 CNN、多层 CNN 或者别的什么？

其中第三列的 Fine Tune 如果为 Y 则说明在测试时，会在测试集的 support set 上进行微调，然后再在 query set 上预测，下同。

由于 Omniglot 数据集比较简单，所以这里的 MATCHING NETS 没有使用 FCE。

在 ImageNet 上做实验时，由于 ImageNet 太大，不方便实验，所以实际上作者是从 ImageNet 中按每类 600 个样本采样了 100 个类得到了 60000 个样本组成的更小的数据集，作者称之为 miniImageNet。其中 80 个类用来做训练，剩下 20 个类用来做测试。

下面是在 miniImageNet 上的对比结果：

我的疑惑：为什么这里就不用 MANN、CONVOLUTIONAL SIAMESE NETS 两个模型来对比了，是不是因为这两个模型的效果都比 MATCHING NETS 好，被打脸了？

除了在 miniImageNet 上做实验外，作者也尝试在完整的 ImageNet 上做实验，但做了一些特殊的设置

• 从 ImageNet 中随机去除了 118 个类别作为训练集，称之为 randImageNet，测试时在那 118 个类别的数据上进行
• 从 ImageNet 中去除狗狗相关的所有类别共 118 个，用剩下的作为训练集，称之为 dogsImageNet，测试时在 118 个狗狗类别的数据上进行

对比的模型除了 PIXELS，还有就是两个 INCEPTION 的分类器

• INCEPTION CLASSIFIER: 在去除 118 个类别后的数据上训练，然后同 BASELINE CLASSIFIER 一样，在测试时只用模型来输出图像的向量表示，得到向量表示后用进行匹配
• INCEPTION ORACLE: 用完整的 ImageNet 进行训练，测试时同 INCEPTION CLASSIFIER

同时，由于从头训练会比较慢，所以 MATCHING NETS 直接使用训练好的 INCEPTION CLASSIFIER 来计算图像特征，在这个基础上再去训练 MATCHING NETS。

结果如下：

注：表中的 \(\neq L_{rand}\) 和 \(\neq L_{dogs}\)表示训练集，，\(L_{rand}\) 和 \(L_{dogs}\) 表示测试集。

从表中可以看到，MATCHING NETS 在 dogsImageNet 上表现是比较差的，对此作者的猜测是训练时只去除狗狗的类别，对数据的分布产生了较大的影响，导致训练集上的数据分布和测试集上的数据分布差异很大，从而表现出了较差的结果。说白了，领域迁移性、泛化性差呗……

最后用 Penn Treebank 做了一个类似语言模型的实验，大致是这样的：

• 给定 support set，里面有 5 条句子，每个句子都被挖了一个空，并给出了这个空要填的词是什么
• 给定一个被挖掉一个词的句子，预测要填入的词，是 support set 中哪个被挖掉的词

如下所示：

有点像语言模型，有点像阅读理解，但又都不是，奇奇怪怪的。

和 LSTM 语言模型做的对比：LSTM 语言模型能达到 72.8% 的效果；本文的模型，在 one-shot 的时候效果为 32.4%，2-shot 的时候是 36.1%，3-shot 的时候是 38.2% —— 就比瞎猜的 20% 高一点点吧。

首先，放到现在来讲，这个 MATCHING NETS 的结构在 NLP 领域是很常见的，就是一个常规的匹配模型啊，不同之处在于使用 FCE 的时候它会用整个 support set 去做 attention，但这也不是什么新奇的东西。当然了这篇论文是 2016 年的，那个时候无论是 attention 机制还是我刚说的匹配模型，可能都还是挺创新的吧。

然后就是论文在一些细节上有没说清楚的，这个我已经在前面用「我的疑惑」这样的字眼指出来了。

• 虽然 Few-Shot Classification 很难，但人类具备很强的这种能力，甚至在某类事物只见过一次后就能在之后非常精准地辨认出来

  嗯，这些论文都这么说，但也没见有引用哪怕一篇认知科学方面的论文来说明这点 —— 成年人见过一次新事物就能辨认出来我是相信的，但婴儿从出生后到什么阶段才具备这种能力呢？我对这个还是比较好奇的，总之对这种抛出一个看起来大家都认可的但没什么实质内容的观点感到无趣。

• Vinyals 提出的 Matching Networks 可以视作一个在 embedding 空间中的加权最近邻分类器

  FCE 是 Matching Networks 里比较精髓的一个设计，虽然整个模型要说是一个最近邻分类器也没错，但这么说未免有点简化过头，而且当前这篇论文提出的 Prototypical Networks，也可以说是一个 embedding 空间中的加权最近邻分类器啊……没有营养的话……

• Vinyals 提出的 episode 的概念让训练结果更加可信、更具有泛化性了

  我不知道在 Vinyals 提出基于 episode 的训练流程之前，做 Few-Shot Learning 的学者们都是怎么做的，但毫无疑问的是这套流程已经在之后成为了一个标准了。

• 在 Prototypical Networks 中，距离度量的选择至关重要，实验表明选择欧式距离比余弦距离好得多

  后面有一堆推论，不是很能看懂。

一个假设: 每个类别都能在空间中对应到一个类比为「原型」的点上，该类的其他数据的表示以这个点为中心分布。

如上图所示，模型要做的事情是将 support set 中的数据映射到一个 embedding 空间中，然后对同类数据的 embedding 平均作为原型的 embedding；同时在预测的时候将输入数据也映射到这个 embedding 空间中，计算与各个原型的距离后，选择距离最小的类别作为预测结果。也就是说，这个模型的重点是：

• 训练一个 encoder
• 选择合适的距离度量方法

下面是模型的具体说明。

给定一个 support set \(S=\{(x_{1}, y_{1}),\ldots, (x_{N},y_{N})\}\)，其中 \(x_{i} \in \mathbb{R}^{D}\) 是一个 \(D\) 维的向量，而 \(y_{i}\in \{1,\ldots, K\}\) 表示 \(K\) 个类别中的一个。特别的，\(S\) 中所有第 \(k\) 类组成的子集记为 \(S_{k}\)。

然后，第 \(k\) 个类别的原型，就可以表示为：

\[c_{k} = \frac{1}{|S_{k}|}\sum\limits_{(x_{i},y_{i})\in S_{k}}f_{\phi}(x_{i})\]

其中 \(f_{\phi}: \mathbb{R}^{D}\rightarrow \mathbb{R}^{M}\) 就是要学习的 encoder。

预测的时候，选定一个距离函数 \(d: \mathbb{R}^{M}\times\mathbb{R}^{M} \rightarrow \left[0,+\infty\right)\)，然后对给定的输入 \(x\) 按如下方式进行预测：

\[p_{\phi}(y=k|x)= \frac{exp(-d(f_{\phi}(x), c_{k}))}{\sum_{k^{\prime}}(-d(f_{\phi}(x), c_{k^{\prime}}))}\]

对应的，训练的目标就是最小化损失函数 \(J(\phi) = -\mathop{log}p_{\phi}(y=k|x)\)。

下面是训练过程的伪代码描述：

注：这篇论文还做了一部分 Zero-Shot Learning 的实验，这个和 Few-Shot Learning 的细节还是有一点区别，我这篇文章专注于 Few-Shot Learning，所以 zero-shot learning 部分的内容暂且忽略，有需要的可以自行阅读论文。

在 Omniglot、miniImageNet 两个数据集上进行了 Few-Shot Learning 的实验。

在 Omniglot 数据集上做实验时，对模型做如下设置：

1. 使用一个四层的 CNN 作为 \(f_{\phi}\)
2. 每层由 64 个 3x3 的卷积核组成，并使用 Batch Normalization，激活函数用 ReLU，最后来一个 2x2 的 max-pooling
3. 使用 Adam 优化算法
4. 学习率初始化为 \(10^{-3}\)，每 2000 个 episodes 裁剪一半

实验结果如下表所示：

这个实验没有和其他模型做对比 —— 可能是各个算法在这个数据集上的效果都能比较轻松地达到 90% 多吧。

作者从这个实验得到这么两个结论：

1. 训练和测试时 support set 中的类别数比测试时的多，会带来更好的效果，这个从上面的表可以很清晰的看出来：1-shot 时 60-way 的效果好于 20-way 好于 5-way，5-shot 时也是同样的。

2. 训练和测试时每类中样本的数量一样会比较好 —— 这我倒看不出来，不知道是不是我理解的不对，原文是这样的

   We found that it is advantageous to match the training-shot with the test-shot.

在 miniImageNet 数据集上做实验时，因为要和 Matching Networks 做对比，所以采用了同样的数据集划分方式。模型设置仍然和前一个实验一样使用四层 CNN。

实验结果如下：

作者从实验中得到的结论是：

• 使用欧式距离比余弦距离要好，这个结论不光是对 Prototypical Networks 而言，甚至在 Matching Networks 上也成立；
• 进行 N-way k-shot 训练时，N 的值越大，总体上看来模型效果会越好，可能是因为训练时类别数多会导致模型能更好地学习到不同类别之间的细微差别，从而提高了泛化性

作者在论文中不厌其烦地说自己的方法是 simple method，我觉得确实如此，其模型结构一目了然，非常直白。作者在文中有说到这么一句话：

We hypothesize this is because all of the required non-linearity can be learned within the embedding function.

也就是说，为什么简单的方法也会有效，很大的成分还是因为模型学到了一个很好的表示。那么，如果将 encoder 的部分替换成一个表示学习能力更强的模块，是不是就能做到更好的效果？我觉得是的。

• 之前的一些工作将工作重心放在学习一个好的数据表示上，然后使用一个已有的度量方法来进行分类，如果距离度量（或相似度量）也通过训练得到，可以得到泛化性更好的模型

• 一些 meta learning 的方法在用于 Few-Shot Learning 问题时，都需要在新的数据上进行 fine tuning 才能得到较好效果，而本文提出的模型可以无需更新模型参数就能用于新类别数据的预测

  这个观点可以分几方面来看

  1. 我这个模型哪怕不 fine tuning 也能表现不错
  2. 提到的那几个 meta learning 的模型不 fine tuning 效果就不行

  对于第一点，看后面的实验结论即可，不过第二点在这篇论文中就看不到什么有力的证据了。

• 与本文工作最接近的是 Prototypical Networks 和 siamese networks

  其实我觉得和 Matching Networks 也很像啦。

Relation Network(RN) 模型由 embedding 模块 \(f_{\varphi}\) 和 relation 模块 \(g_{\phi}\) 组成，如下图所示：

对比一下这张图和 Matching Networks 的结构图，实在是太像了。

具体来说

• embedding 模块使用 4 层 CNN，每层 64 个 3x3 的卷积核，使用 Batch Normalization，激活函数用 ReLU —— 基本上和 Matching Networks、Prototypical Networks 是一样的，不过稍有区别，就是这里的 embedding 模块的后两层 CNN 没有加 max pooling，这个是为了适配 relation 模块做的修改

• relation 模块用来将 support sample 和 query sample 的 feature map 融合起来并计算匹配分数

  因此首先有一个拼接函数 \(C(\cdot, \cdot)\)，这个函数将两个 feature map 在 depth 通道上拼接起来。

  拼接起来后再通过一个 \(g(\phi)\) 进行融合并计算分数。

  对一个 N-way 1-shot 的任务，在给一个 query sample \(x_{j}\) 的时候，会得到 N 个分数：

  \[r_{i,j} = g_{\phi}(C(f_{\varphi}(x_{i}), f_{\varphi}(x_{j})))\qquad i=1,2,\ldots, N\]

  如果是 N-way K-shot 任务且 \(k > 1\)，则把 support set 中同一类的 embedding 简单加起来再输入到 relation 模块中 —— 这里我有一个疑问，同一类的多个样本的 embedding 加起来后不平均一下吗？

  此处的 \(g_{\phi}\) 是两层 CNN 再加上两层全连接层。

模型的总体结构如下图所示：

训练时使用 MSE 作为 loss。

完了，模型上可以说也是比较简单直白的。

和前两篇论文一样在 Omniglot 和 miniImageNet 两个数据集上做的实验。

统一的训练设置

• 使用 Adam 优化算法
• 初始学习率置为 0.001
• 每 10 万个 episodes 后对学习率进行裁剪

在 Omniglot 数据集上实验时，有如下额外设置：

• 训练时的数据采样设置
  • 5-way 1-shot 时，query set 中每个类别有 19 张图片
  • 5-way 5-shot 时，query set 中每个类别有 15 张图片
  • 20-way 1-shot 时，query set 中每个类别有 10 张图片
  • 20-way 5-shot 时，query set 中每个类别有 5 张图片
• 测试时，从 test set 中采样了 1000 个 episodes，将这 1000 个 episodes 的测试结果平均作为整体测试结果

实验结果如下：

在 miniImageNet 数据集上实验时，有如下额外设置：

• 训练时的数据采样设置
  • 5-way 1-shot 时，query set 中每个类别有 15 张图片
  • 5-way 5-shot 时，query set 中每个类别有 10 张图片
• 测试时，对 600 个 episodes 的结果平均作为整体结果

实验结果如下：

此外还有 zero shot learning 的实验，略。

从结果上来看，Relation Networks 的效果并没有显著好于 Matching Networks 和 Prototypical Networks，在 miniImageNet 上的 5-way 5-shot 设置时甚至还比 Prototypical Networks 差一些。不过我觉得这个思路是没有问题的。

以及，可以看到各个方法都能轻松在 Omniglot 数据集上达到 99% 的准确率，所以这个数据集其实已经没有什么参考意义了……倒是各个模型在 miniImageNet 上都还有很大的提升空间。

• 之前的一些工作在计算一个类别的 representation 的时候，只是简单的将这个类的 support sample 的 representation 加起来或平均一下，这样做可能会丢失一些重要的信息

  不对哦，Matching Networks 那里用的 FCE 已经是很接近 attention 的思路了，可不是将 support sample 的 representation 简单加起来或平均的。

• 一个 Few-Shot Classification 的任务，如果有足够多的类别供训练，那么过拟合的风险会比较低。

  文中说这个的时候举了一个例子：假设一个数据集中有 159 个训练用类别，按 5-way 的设置来训练的话，也就是从 159 个类里选 5 个类用于训练，这样可以有 794747031 种不同的子任务。

  我在想啊，这个想法能不能借鉴到普通的匹配任务上。在如检索式问答一类的匹配任务上，通常是做二分类，也就是选两个样本，判断他们是否属于同一类。而当 \(N > 3\) 且 \(k>2\) 的时候，组合数 \(C^k_{N}\) 总是比 \(C^{2}_{N}\) 大，所以如果借鉴 Few-Shot Learning 里的 episode 的思想的话，就能得到更多的训练机会；其次，原来在匹配的时候，对于负样本之间（可能属于不同的问题簇）是不做区分的，区分一下的话感觉也会有好处。

上图是一个 3-way 2-shot 的模型结构示例图。

模型由 Encoder 模块、Induction 模块和 Relation 模块组成。 Encoder 模块是双向 LSTM，加上 self attention —— 给定输入文本 \(x=\left(w_{1}, w_{2}, \ldots, w_{T}\right)\)，最终得到一个向量 \[e = \sum_{t=1}^{T}a_{t}\cdot h_{t}\]

其中 \(h_{t}\) 是一个 biLSTM 的 hidden state：

\[\overrightarrow{h_{t}} = \overrightarrow{LSTM}(w_{t}, h_{t-1})\]

\[\overleftarrow{h_{t}} = \overleftarrow{LSTM}(w_{t}, h_{t+1})\]

\[h_{t} = concatenate(\overrightarrow{h_{t}}, \overleftarrow{h_{t}})\]

而 \(a_{t}\) 是 attention 权重，所有 \(a_{t}\) 组成的向量 \(a\) 是这样计算出来的：

\[a = softmax(W_{a2} tanh(W_{a1} H))\]

其中 \(W_{a1} \in R^{d_{a}\times 2u}\)，\(W_{a2}\in R^{d_{a}}\)，\(H = \left[h_{1} \ldots h_{T}\right]\) 表示由所有 \(h_{t}\) 组成的矩阵， \(2u\) 是 \(h_{t}\) 的向量长度，\(d_{a}\) 是超参数。

Induction 模块要做的是将 \(C\times K\) 个 support sample 的向量表示 \(e\) 转换成 \(C\) 个类的向量表示 —— 之前的一些工作在这里大都是通过将一个类中的 support sample 的向量表示平均或相加得到。这篇论文创新的地方是，在 Induction 模块这里，用了胶囊网络里的动态路由机制⁷。

胶囊网络我不是太懂，暂时也没太多兴趣和精力去看 Hinton 那篇论文。论文中列出了 Induction 模块的计算过程，还是比较清楚的，如下图所示：

可以理解为在计算类的向量表示的时候，对这个类中的 support sample 做了加权，然后不同的 support sample 的权重是靠这个动态路由机制来计算的，其中所需的一些参数（如 \(W_{s}\) 和 \(b_{s}\)）也是在训练中得到的。

最后的 Relation 模块，用来比对 query sample 也就是待预测的样本和每个类的向量表示 \(c_{i}\)，以判断这个 query sample 应该被分到哪个类上。

Relation 模块首先用一个张量网络⁸来建模两个向量（也就是 query sample 的向量和类向量 \(c_{i}\)）的关系，然后再经过一个全连接层输出匹配分数：

\[v(c_{i}, e^{q}) = f(c_{i}^{T}M^{\left[1:h\right]}e^{q})\]

\[r_{iq} = sigmoid(W_{r}v(c_{i}, e^{q}) + b_{r})\]

训练时的目标函数则为：

\[L(S, Q) = \sum\limits_{i=1}^{C}\sum\limits_{q=1}^{n}(r_{iq} - \mathbf{1}(y_{q} == i))^{2}\]

训练时候使用的优化算法是 Adagrad⁹。

在两个数据集上做了实验，一个是 Amazon Review Sentiment Classification 数据集（简称为 ARSC 数据集），另外一个是阿里巴巴整理出来的 Open Domain Intent Classification for Dialog System 数据集（简称为 ODIC 数据集）。

两个实验都和这些模型进行对比：Matching Networks, Prototypical Networks, Relation Networks, Graph Network¹⁰, SNAIL¹¹, ROUBUSTTC-FSL¹²。

ARSC 数据集是在不同的电商产品类型上的评论数据，每个数据会被标记为正向、负向和不确定三个类别，总共有 23 个产品类型，所以加起来有 69 个类别。在该数据上实验时，设置如下：

• 将四个产品的 12 个类别作为 test set，剩下产品的 57 个类别作为 train set
• 使用 300 维的 Glove embedding
• LSTM 的 hidden state size 设置为 128
• 计算 self attention 时的超参 \(d_{a}\) 设置为 64
• 训练时 support set 为 2-way 5-shot

实验结果如下：

ODIC 数据集有 216 个类别，将其中 159 个类别共 195775 个样本作为 train set，剩下 57 个类别共 2279 个样本作为 test set。在该数据集上实验时，设置如下：

• 使用 300 维的中文 word embedding
• LSTM 的 hidden state size 和 self attention 的超参同 ARSC 数据集
• 分别进行了 5-way 5-shot、5-way 10-shot、10-way 5-shot 和 10-way 10-shot 四种实验
• 测试时，在 test set 上采样 600 个 episode 进行测试，然后将平均测试结果作为整体结果

在 ODIC 数据集上的实验结果如下所示：

除了两个对比实验外，论文还做了一些模型的分析。

第一个分析是尝试将 Induction Networks 中的部分模块替换为更简单的模块，看模型的最终效果变化，来衡量这个模块是否有效。结果如下：

上图中前三行是 Induction Networks 自己的结果，后面三行就是替换其中部分模块或的结果，其中：

• 第四行表示将 Relation 模块替换为简单的余弦相似方法
• 第五行表示将 Induction 模块替换为将类中向量加和作为 \(c_{i}\) 的方法
• 最后一行表示用 Attention 替代 Induction 模块 —— 文中说是 self attention，应该是指在计算一个类内 support sample 的权重时，对该类内所有的 support sample 进行 attention 计算来得到权重

可以看到，直接使用 Attention 替代 Induction 模块，比 Induction 模块不做迭代要好一点点，但三步迭代后本文模型还是会好一些。

然后还有一些可视化的分析，都是在论证 Induction Networks 比其他模型要好，这里不一一列举了。

论文声称的「其他方法都是将 support sample 的向量表示简单加起来或平均作为」其实并不是事实，早在 2016 年的时候提出 Matching Networks 的论文中所使用的 Full Context Embedding 即 FCE 的目标和这篇论文里的 Induction 模块就是一样的，无非是方法不同而已。

借鉴胶囊网络思路的那个 Induction 模块还有点意思。

ODIC 数据集好像没有开放出来，遗憾。

• Few-Shot Classification 虽然在最近取得了不少进展，但是各个方法由于复杂的模型设计和不同的实现细节，导致他们很难互相比较
• Few-Shot Classification 所使用的 baseline 方法效果被显著地低估了

• 目前的 Few-Shot Classification 模型评估，都是从同样的数据集中采样出来进行的，导致模型的领域迁移性较低

  我理解之所以这么说，是因为 Few-Shot Learning 本来宣称的一个目标就是能应付新的类别的数据，而如果这个所谓的「新的类别」必须是在同一个领域内的，那么其实会很受限制。

  这点在 Matching Networks 那篇论文里也有提到。

这篇论文的目标不是提出一个新的模型来在 Few-Shot Classification 问题上得到更好的效果，所以在模型部分，只是对一个简单的 baseline 模型做了增强得到了 baseline++ 模型，用来在之后和其他模型对比，以论证前面的「baseline 方法效果被显著低估了」这个观点。

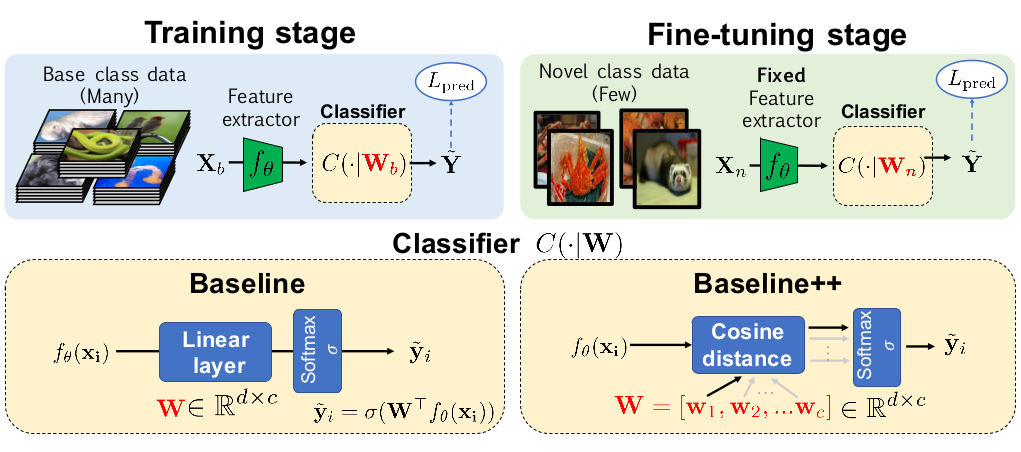
如上图所示，baseline 模型由一个 feature extractor 或者说 encoder 和一个分类模块组成，作者之所以认为之前的一些工作里 baseline 模型效果被低估了，是因为之前的一些论文，在分类模块这里，用的是一个固定的、简单的距离函数（如余弦距离、欧式距离）。

作者在这里做了一些改动，包括：

• baseline 模型的分类模块使用一个全连接层，训练好后，用于新类别数据时，会用新的 support set 进行 fine tuning （之前一些工作里是不做的）

• baseline++ 在 baseline 模型的基础上对全连接层的计算做了简单的调整

  记权重矩阵 \(\mathbf{W} = [\mathbf{w}_{1}, \mathbf{w}_{2}, \ldots, \mathbf{w}_{c}]\)，最终分类模块会输出一个长度为 \(c\) 的向量，表示预测为各个类别的概率，记为 \(\mathbf{s} = [s_{1}, s_{2}, \ldots, s_{c}]\)。

  在 baseline 模型里，是这么计算的：\(\mathbf{s} = softmax(\mathbf{W}^{T}f_{\theta}(x))\)

  而在 baseline 模型里，则是这么计算的：\(s_{i} = \frac{f_{\theta}(x)^{T}\mathbf{w}_{i}}{\parallel f_{\theta}(x) \parallel\parallel \mathbf{w}_{i} \parallel}\)

当然，作者在这里强调，这个 baseline++ 模型并不是他们的贡献，而是来自于 2018 年的一篇论文¹⁴。

作者对比了 Matching Networks、Prototypical Networks、Relation Networks 和一个 meta learning 的方法 MAML 模型。

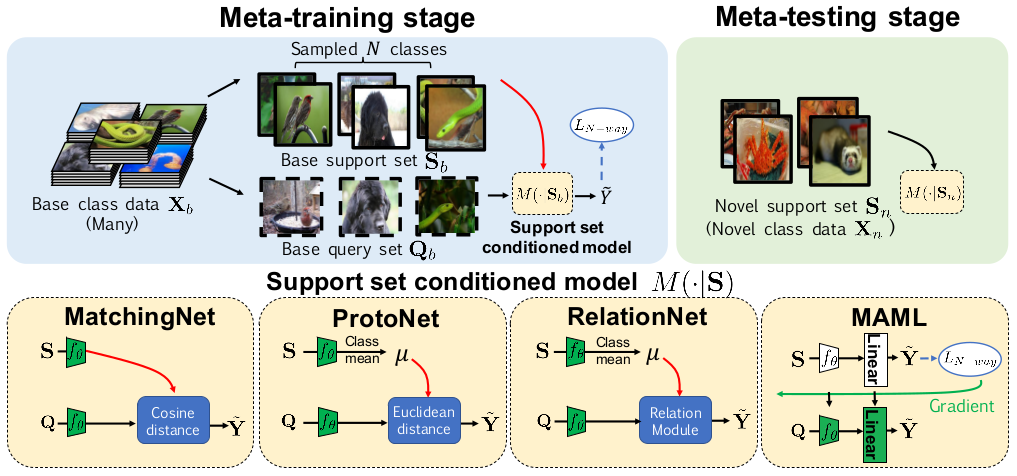
这个对比图还是挺直观的，对于理解不同模型之间的差异挺有帮助。

图上的 meta-training 和 meta-testing，其实就是指训练和测试。但是 Few-Shot Classification 的训练用数据和实际使用是要预测的类别原则上是不一样的，学到的更多的是区分不同类别的能力而不是区分某个指定类别的能力，这个还有监督分类问题是不太一样的，这里加个 meta 是和普通的分类模型的训练、测试进行区分，不用太在意。b

进行了三个实验：

• 使用 miniImageNet 数据集进行一般的图像分类实验
• 使用 CUB-200-2011 数据集（后面简称为 CUB 数据集）进行细粒度图像分类实验
• 使用 miniImageNet 数据集训练，在 CUB 数据集上进行验证和测试，对比各个模型的跨领域适应能力

实验的通用设置为：

• 分别进行 5-way 1-shot 和 5-way 5-shot 实验，训练时的 query set 每类 16 个样本
• 对 1-shot 实验，训练 60000 个 episodes；对 5-shot 实验，训练 40000 个 episodes
• 测试时，将 600 个 episodes 上测平均测试结果作为整体结果
• baseline 模型和 baseline++ 模型训练时设置 batch size 为 16，训练 400 个 epochs
• baseline 模型和 baseline++ 模型，在测试时，让 encoder 参数不变，用 support set 对分类模块进行 fine tuning，batch size 设置为 4 训练 100 次
• 所有模型训练时都使用 Adam 优化算法，初始学习率设置为 0.001

由于作者自己重新实现了用于对比的几个模型，所以先和原作者论文中报告的结果做了对比，如下图所示：

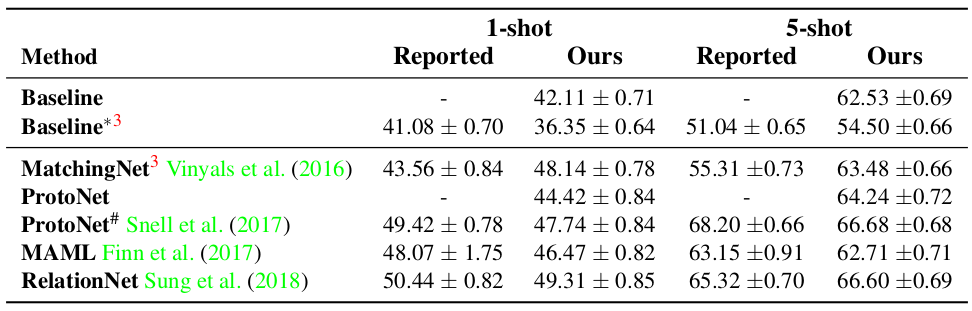
可以看到作者实现的这几个模型和它们的原实现的效果相比，大部分是稍差一些，也有些表现更好的。

在 CUB 和 miniImageNet 两个数据集上做实验时，使用四层 CNN 作为 encoder，实验结果如下图所示：

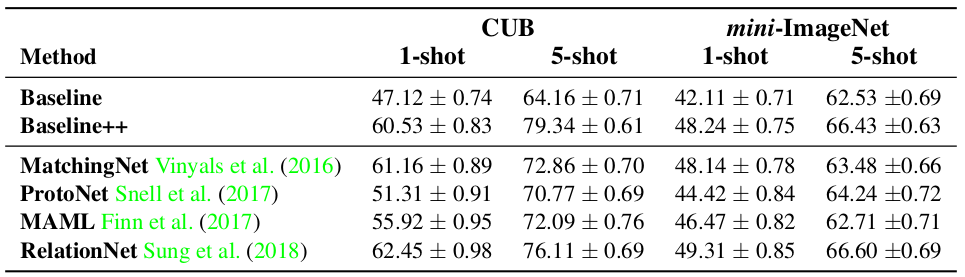
可以看到，baseline++ 模型和这些 SOTA 的模型相比并没有很大的差距，甚至在一些情况下比 SOTA 的模型还要好。baseline++ 模型仅仅是对 baseline 模型的一个简单修改，所以作者说 baseline 模型的能力被显著地低估了。

接着，作者认为 encoder 是很重要的，所以尝试了将 encoder 替换成更深的网络，结果显示使用更深的网络后大部分模型的效果都有了显著的提升。

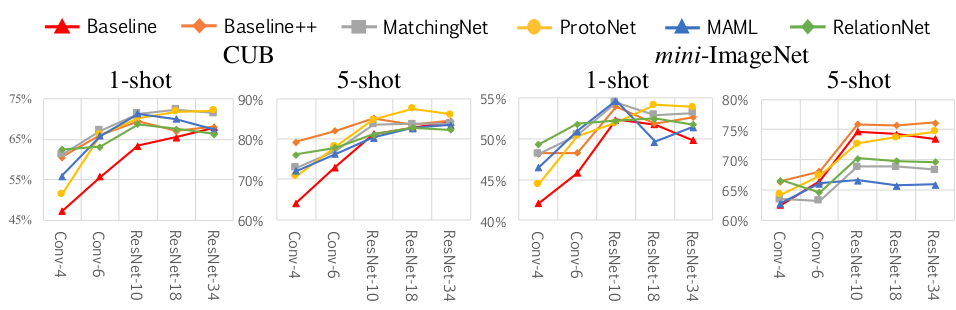
第三个实验 —— 也就是那个先在 miniImageNet 数据集上训练然后在 CUB 数据集上测试的实验，统一使用更深的 ResNet-18 作为 encoder，结果显示 baseline 模型的效果最好。

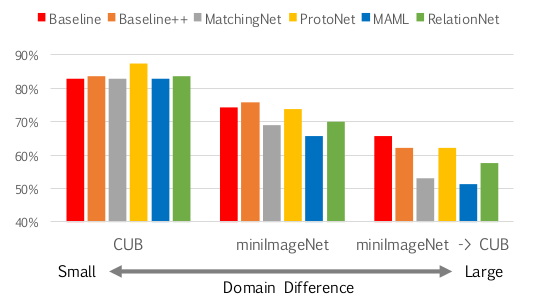
由于 CUB 数据集都是鸟类的数据，所以训练与测试时的领域差异性很小；miniImageNet 数据集包含了很多不同类别的物体，所以领域差异性比 CUB 要大；当训练使用 miniImageNet 数据集而测试时使用 CUB 时，领域差异性是最大的。同样使用 ResNet-18 作为 encoder 时，三个不同的 5-way 5-shot 实验对比结果也说明了目前这些 Few-Shot Classification 模型在领域迁移上的问题，如下图所示：

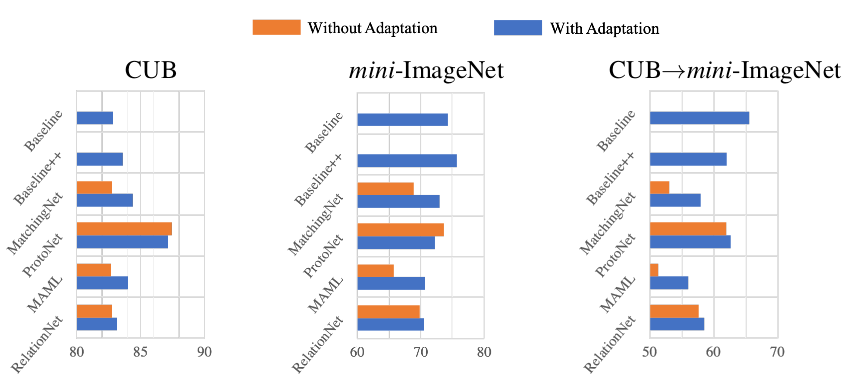
而之所以 baseline 模型会最好，有可能是因为 baseline 模型进行了 fine tuning，所以作者再进一步实验，在其他模型上也加上 fine tuning 操作，结果显示领域差异性大时，fine tuning 是很有必要的，如下图所示：